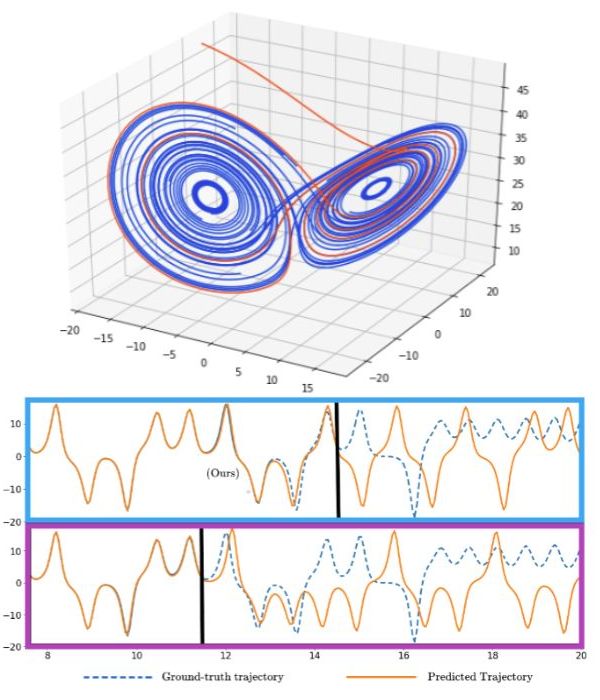
The understanding of chaotic systems is challenging not only for theoretical research but also for many criticalapplications. Chaotic behavior is found in many nonlinear dynamical systems, such as climate dynamics, weatherprediction, and the space-time dynamics of virus spread. A reliable solution for these systems must handle theircomplex space-time dynamics and sensitive dependence on initial and boundary conditions.

We develop a deep learning framework to push the time horizon at which reliable predictions can be made furtherinto the future by better evaluating the consequences of local errors when modeling nonlinear systems[1]. Ourapproach observes the future trajectories of initial errors at a time horizon to model the evolution of the lossto that point with two major components:

• a recurrent architecture (Error Trajectory Tracing) based on thecalculation of the Lyapunov exponent, designed to trace the trajectories of predictive errors through phase space,and
• a training regime, Horizon Forcing, that pushes the model’s focus out to a predetermined time horizon.

Wevalidate our method on three classics, chaotic systems, and four real-world time series prediction tasks with chaoticcharacteristics, and our approach outperforms the current state-of-the-art methods.